Мазмұны:
Бейне: Теңдеудің түбірлерін алгебралық жолмен қалай табуға болады?
2024 Автор: Miles Stephen | [email protected]. Соңғы өзгертілген: 2023-12-15 23:38
The тамырлар кез келген квадраттың теңдеу берілген: x = [-b +/- sqrt(-b^2 - 4ac)]/2a. Квадратты ax^2 + bx + c = 0 түрінде жазыңыз. Егер теңдеу y = ax^2 + bx +c түрінде болады, жай ғана y-ді 0-ге ауыстырыңыз. Бұл орындалады, себебі тамырлар -ның теңдеу у осі 0-ге тең мәндер.
Сонымен қатар, графикте функцияның түбірлерін қалай табуға болады?
А тамыр берілген мән болып табылады функциясы нөлге тең. Бұл кезде функциясы а бойынша сызылған график , the тамырлар нүктелері болып табылады функциясы х осін кесіп өтеді. Үшін функциясы , f(x), the тамырлар f(x)=0 f (x) = 0 болатын х мәндері.
Сонымен қатар, теңдеудің түбірлерінің қосындысы неге тең? Бұлар деп аталады тамырлар квадраттың теңдеу . Квадрат үшін теңдеу балта2+bx+c = 0, the сома оның тамырлар = –b/a және оның көбейтіндісі тамырлар = с/а. Квадрат теңдеу екі биномның көбейтіндісі ретінде өрнектелуі мүмкін.
Сонда теңдеудің неше түбірі бар?
Бұл x=0 мыналардың бірі екенін білдіреді тамырлар . Дәреже 3, сондықтан біз 3 деп күтеміз тамырлар . Бір ғана мүмкін комбинация бар: 3 тамырлар : 1 оң, 0 теріс және 2 комплекс.
Көпмүшелік өрнектерді қалай шешесіз?
Қадамдар
- Сізде сызықтық көпмүше бар-жоғын анықтаңыз. Сызықтық көпмүше - бірінші дәрежелі көпмүше.
- Теңдеуді нөлге теңестіріңіз. Бұл барлық көпмүшелерді шешу үшін қажетті қадам.
- Айнымалы терминді оқшаулаңыз. Ол үшін теңдеудің екі жағынан тұрақты мәнді қосу немесе азайту керек.
- Айнымалы үшін шешіңіз.
Ұсынылған:
Логарифмдік теңдеудің асимптотасын қалай табуға болады?
Негізгі нүктелер Графикті түсіргенде логарифмдік функция пішіні бойынша квадрат түбір функциясына ұқсас, бірақ х оң жақтан 0-ге жақындаған кезде тік асимптотасы бар. (1,0) нүктесі y=logbx y = l o g b x түріндегі барлық логарифмдік функциялардың графигінде орналасқан, мұндағы b оң нақты сан
Абсолютті мән теңдеуін алгебралық жолмен қалай шешесіз?
ҚҰРАМЫНДА АБСОЛЮТТЫ МӘН(тер) БАР ТЕҢДЕЛЕРДІ ШЕШУ 1-қадам: Абсолютті мән өрнегін оқшаулаңыз. 2-қадам: абсолютті мән белгілеуінің ішіндегі шаманы + және - теңдеудің екінші жағындағы шамаға тең етіп орнатыңыз. 3-қадам: Екі теңдеуде де белгісізді шешіңіз. 4-қадам: Жауабыңызды аналитикалық немесе графикалық түрде тексеріңіз
Параметрлік теңдеудің бағдарын қалай табуға болады?
Параметр өскен сайын жазықтық қисығының бағыты қисық бағдары деп аталады. Жазық қисықтың бағытын қисық бойымен сызылған көрсеткілер арқылы көрсетуге болады. Төмендегі графикті қарастырыңыз. Ол x = cos(t), y = sin(t), 0≦t < 2&Pi параметрлік теңдеулерімен анықталады;
Сызықтық теңдеулер жүйесін алгебралық жолмен қалай шешесіз?
Екі теңдеудегі ортақ шешімді шешу үшін жоюды пайдаланыңыз: x + 3y = 4 және 2x + 5y = 5. x= –5, y= 3. Бірінші теңдеудегі әрбір мүшені –2-ге көбейтіңіз (сіз –2x – аласыз) 6y = –8), содан кейін екі теңдеудегі мүшелерді бірге қосыңыз. Енді у үшін –y = –3 мәнін шешіңіз, сонда сіз у = 3 аласыз
Алгебралық функцияның анықталу облысын қалай табуға болады?
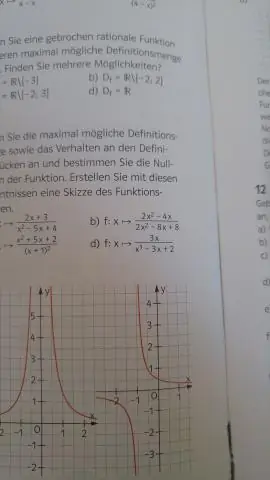
Функцияның анықталу облысы – функцияның барлық мүмкін болатын кірістерінің жиыны. Мысалы, f(x)=x² анықталу облысы барлық нақты сандар, ал g(x)=1/x анықталу облысы x=0-ден басқа барлық нақты сандар