Бейне: Шеңбердің радиусы нөлге тең бола ала ма?
2024 Автор: Miles Stephen | [email protected]. Соңғы өзгертілген: 2023-12-15 23:38
Менің білуімше, а анықтамасында ештеңе жоқ шеңбер бұл оның екенін көрсетеді радиусы болмайды нөл … дегенмен, а шеңбер бірге радиусы нөл көптеген қасиеттерін жоғалтады шеңберлер . Бірақ а шеңбер а радиусы ның нөл басқасына масштабтауға болмайды радиусы.
Осыны ескере отырып, радиусы 0 болатын шеңбер дегеніміз не?
Егер радиусы нөл болса, онда ол шын мәнінде а емес шеңбер , бірақ азғын деп атауға болады шеңбер --яғни, егер сіз а анықтамасын сәл ұзартсаңыз, не аласыз шеңбер бірдей теңдеуді қолдану арқылы, бірақ оны жасау арқылы шектен шығу радиусы нөл.
Содан кейін сұрақ туындайды, шеңбер радиустан кіші болуы мүмкін бе? Иә, а шеңбер болады кез келген оң бар радиусы . А шеңбер а радиусы ның одан азырақ бүйірінің ұзындығы бір шаршы сияқты проблемасыз одан азырақ бір.
Сондай-ақ біліңіз, шеңбердің радиусы теріс болуы мүмкін бе?
Иә, радиусы теріс болуы мүмкін , бұл оның көрсетілген жағына мүлдем қарама-қарсы бағытта өлшенетінін білдіреді шеңбер . Егер радиусы нөл болса, а артық емес шеңбер бірақ бұл нүкте.
Нүктелік шеңбердің радиусы неге тең?
a үшін жалпы теңдеу шеңбер x2+y2+2gx+2fy+c=0, мұндағы h=−g және k=−f. The радиусы онда r=√g2+f2−c. Егер g2+f2−c=0 болса, онда бұл а нүктелі шеңбер . Егер g2+f2−c>0 болса, онда бұл нақты шеңбер.
Ұсынылған:
Неліктен магнит ағыны максималды болғанда индукцияланған ЭҚК нөлге тең болады?
Катушка тік тұрған кезде магнит ағынында ешқандай өзгеріс болмайды (яғни эмф=0), себебі катушкалар өріс сызықтарын «кесіп өтпейді». Катушкалар өріс сызықтарына перпендикуляр болған кезде индукцияланған ЭҚК нөлге тең, ал параллель болғанда максимум. Есіңізде болсын, индукцияланған ЭҚК - бұл магнит ағынының байланысының өзгеру жылдамдығы
Неліктен катушка магниттің дәл ортасынан өткенде ЭҚК нөлге тең?
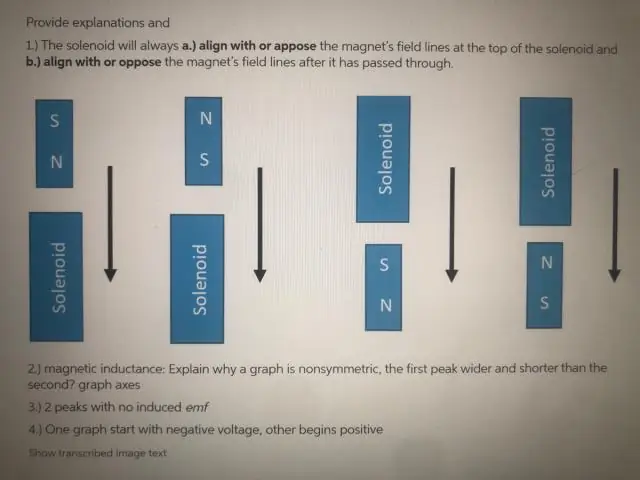
ЭҚК бір сәтке тек нөлге тең, өйткені магнит катушканың дәл ортасынан өтеді. Себебі магниттің бір ұшындағы N полюсінің катушканың сол ұшына әсері магниттің S полюсінің катушканың екінші ұшына әсерімен дәл жойылады
Неліктен элементтердің түзілу энтальпиясы нөлге тең?
Элементтің элементтік күйіндегі түзілу энтальпиясы әрқашан 0 болады, өйткені ол табиғи қосылыс түзу үшін энергияны қажет етпейді. Зат оның элементтерінің ең тұрақты түрінен түзілгенде энтальпияның өзгеруі орын алады
Тең қабырғалы тікбұрышты үшбұрыштың табандық бұрыштары әрқашан 45-ке тең бола ма?
Тең қабырғалы тікбұрышты үшбұрышта тең қабырғалары тік бұрыш жасайды. Тікбұрышты үшбұрыш тең қабырғалы болғандықтан, табанындағы бұрыштары тең болатынын ескеріңіз. (Теорема 3.) Сондықтан бұл сүйір бұрыштардың әрқайсысы 45°
Радиусы 5-ке тең шеңбердің теңдеуі қандай?
Шеңбердің стандартты түрі төменде келтірілген: (x – h)2 + (y – k)2 = r2, мұндағы центр (h, k) нүктесінде орналасқан және r – радиустың ұзындығы. Бұл жағдайда h –3, k – 6, r – 5 болады