Мазмұны:
Бейне: Координаталық геометрияда батпырауықты қалай дәлелдейсіз?
2024 Автор: Miles Stephen | [email protected]. Соңғы өзгертілген: 2023-12-15 23:38
Міне, екі әдіс:
- Егер төртбұрыштың бір-бірінен ажырамайтын екі қабырғасы сәйкес болса, онда ол батпырауық (кері батпырауық анықтамасы).
- Егер төртбұрыштың диагональдарының бірі екіншісінің перпендикуляр биссектрисасы болса, онда ол батпырауық (қасиетке қарсы).
Кейіннен, батпырауықтың ерекшеліктері қандай?
Батпырауық қасиеттерге (1) екі жұп дәйекті, конгруент қабырғалары, (2) конгруент төбесінен емес бұрыштар және (3) перпендикуляр диагональдар жатады. Танысатын басқа маңызды көпбұрыш қасиеттеріне трапеция қасиеттері, параллелограмм қасиеттері, ромб қасиеттері, тіктөртбұрыш пен квадрат қасиеттері жатады.
Тіктөртбұрыш перпендикуляр ма? Сол жақтағы суреттерден көріп тұрғаныңыздай, а диагональдары төртбұрыш тік бұрышта қиылыспаңыз (олар емес перпендикуляр ). (Егер төртбұрыш шаршы болып табылады.) Ал қиылысудан пайда болатын бұрыштар әрқашан бірдей өлшем (өлшем) бола бермейді. Қарама-қарсы орталық бұрыштардың өлшемдері бірдей (олар конгруентті.)
Содан кейін сұрақ туындайды, батпырауық перпендикуляр ма?
АНЫҚТАМА: А батпырауық төрт қабырғасы көршілес екі түрлі жиын болатындай етіп сызылған төртбұрыш, сәйкес жақтары. ТЕОРЕМА: Егер төртбұрыш болса батпырауық , диагональдары перпендикуляр . ТЕОРЕМА: Егер төртбұрыш болса батпырауық , оның бір жұп қарама-қарсы бұрыштары бар сәйкес.
Тіктөртбұрыш параллелограмм ба?
А төртбұрыш екі жұп қарама-қарсы қабырғалары параллель және төрт тік бұрыштары бар. Ол сондай-ақ а параллелограмм , өйткені оның екі жұп параллель жақтары бар.
Ұсынылған:
Координаталық жазықтықта кеңеюдің масштабтық коэффициентін қалай табуға болады?
A(2, 6), B(2, 2), C(6, 2) координаталары бар ABC үшбұрышының графигін салыңыз. Содан кейін кескінді кеңейту орталығы ретінде бастапқы нүктемен 1/2 масштаб коэффициентіне кеңейтіңіз. Алдымен координаталық жазықтықта бастапқы үшбұрыштың графигін саламыз. Әрі қарай, біз әрбір координатты 1/2 масштаб коэффициентіне көбейтеміз
Координаталық жазықтықта теңсіздіктердің графигін қалай саласыз?
Үш қадам бар: «y» сол жақта, ал қалғандары оң жақта болатындай теңдеуді қайта реттеңіз. 'y=' сызығын сызыңыз (оны y≤ немесе y≥ үшін тұтас сызық және y үшін үзік сызық етіңіз) «Үлкен» (y> немесе y≥) үшін сызықтың үстіне немесе а үшін сызықтың астына көлеңке қойыңыз 'кіші' (y< немесе y≤)
Геометрияда координаталық жазықтықты қалай саласыз?
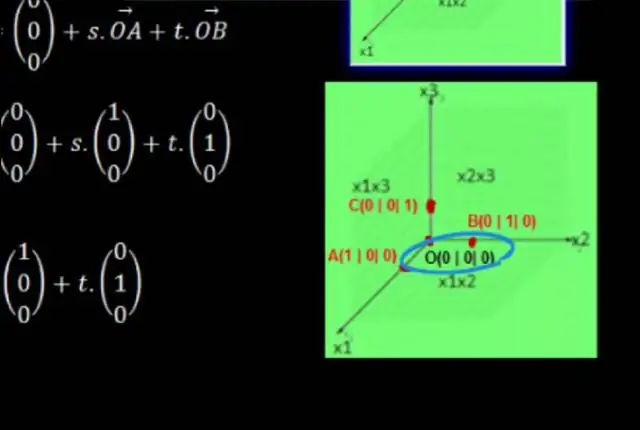
Координаталық жазықтықты құру үшін мына қадамдарды орындаймыз: Екі түзудің де 0 нүктесінде қиылысатын бір-біріне перпендикуляр екі сан түзуін сызамыз. Көлденең сан сызығын x осі деп, ал тік сан сызығын у осі ретінде белгілеңіз
Координаталық жазықтық сәйкес жақтардың конгруент екенін анықтауға қалай көмектеседі?
Координаталық жазықтықта екі үшбұрыш берілген болса, олардың қабырғаларының ұзындықтарын табу үшін қашықтық формуласын пайдалану арқылы олардың сәйкестігін тексеруге болады. Егер үш жұп қабырғалары сәйкес болса, онда үшбұрыштар жоғарыдағы теорема бойынша сәйкес болады
Координаталық жазықтық қалай аталады?
Екі өлшемді жазықтықты декарттық жазықтық деп атайды немесе координаталық жазықтық пен осьтерді координаталық осьтер немесе х осі мен у осі деп атайды. Берілген жазықтықта квадрант деп аталатын басы бойынша төрт бірдей бөлім бар