Мазмұны:
Бейне: Гауссты жою арқылы сызықтық теңдеуді қалай шешесіз?
2024 Автор: Miles Stephen | [email protected]. Соңғы өзгертілген: 2023-12-15 23:38
Гаусс элиминациясын теңдеулер жүйесін шешу үшін қалай қолдануға болады
- Кез келген қатарды көбейтуге болады бойынша тұрақты (нөлден басқа). үшінші қатарды көбейтеді бойынша –2 жаңа үшінші қатарды береді.
- Кез келген екі жолды ауыстыруға болады. бірінші және екінші жолдарды ауыстырады.
- Бірге екі жолды қосуға болады. бірінші және екінші жолдарды қосады және оны жазады жылы екінші қатар.
Сонда Гауссты жою қалай жұмыс істейді?
Жай сөзбен айтқанда, Гауссты жою жұмыстары жоғарыдан төменге қарай эшелон түрінде матрицаны шығару үшін, ал Гаусс - Иордания жою қайда жалғасады Гаусс төмендетілген эшелон түрінде матрицаны шығару үшін төменнен жоғары жұмыс істеуге дейін қалды. Техника келесі мысалда суреттелетін болады.
Сонымен қатар, Крамер ережесінің матрицалары дегеніміз не? Крамер ережесі 2×2 жүйесі үшін (екі айнымалысы бар) Крамер ережесі анықтауыштарды пайдаланып сызықтық теңдеулер жүйесін шешуге болатын тағы бір әдіс. Белгілер бойынша, а матрица while - шаршы жақшаға алынған сандар массиві анықтауыш екі тік жолақпен қоршалған сандар массиві.
Екіншіден, Гауссты жоюдың мақсаты қандай?
Гауссты жою . Википедиядан, еркін энциклопедия. Гауссты жою , сонымен қатар жолды азайту деп те белгілі, сызықтық теңдеулер жүйесін шешуге арналған сызықтық алгебрадағы алгоритм. Ол әдетте коэффициенттердің сәйкес матрицасы бойынша орындалатын операциялар тізбегі ретінде түсініледі.
Гаусс пен Гаусс Джорданды жоюдың айырмашылығы неде?
3 Жауаптар. Гауссты жою матрицаны қатар эшелон түрінде қоюға көмектеседі, ал Гаусс - Иордания матрицаны қысқартылған жол эшелон түрінде қояды. Кішкентай жүйелер үшін (немесе қолмен) әдетте пайдалану ыңғайлы Гаусс - Иорданияны жою және ұсынылған әрбір айнымалы үшін анық шешіңіз ішінде матрицалық жүйе.
Ұсынылған:
Квадрат теңдеуді нөлдік көбейткіштер заңы арқылы қалай шешесіз?
Бұдан мынадай қорытынды шығаруға болады: Егер кез келген екі санның көбейтіндісі нөлге тең болса, онда сандардың біреуі немесе екеуі де нөлге тең болады. Яғни, егер ab = 0 болса, онда a = 0 немесе b = 0 (бұл а = b = 0 мүмкіндігін қамтиды). Бұл нөлдік фактор заңы деп аталады; және біз оны квадрат теңдеулерді шешу үшін жиі қолданамыз
Сызықтық теңдеулер жүйесін графикалық жолмен қалай шешесіз?
Сызықтық теңдеулер жүйесін графикалық жолмен шешу үшін екі теңдеудің бір координат жүйесінде графигін саламыз. Жүйенің шешімі екі түзудің қиылысу нүктесінде болады. Екі түзу осы теңдеулер жүйесінің шешімі болып табылатын (-3, -4) ішінде қиылысады
Үш теңдеу жүйесін жою арқылы қалай шешуге болады?
Екі теңдеудің басқа жинағын таңдаңыз, (2) және (3) теңдеулерін айтыңыз және бірдей айнымалыны жойыңыз. (4) және (5) теңдеулер арқылы құрылған жүйені шешіңіз. Енді у-ді табу үшін (4) теңдеуіне z = 3 мәнін қойыңыз. 4-қадамдағы жауаптарды пайдаланыңыз және қалған айнымалыны қамтитын кез келген теңдеуге ауыстырыңыз
Айнымалыны оқшаулау арқылы теңдеуді қалай шешесіз?
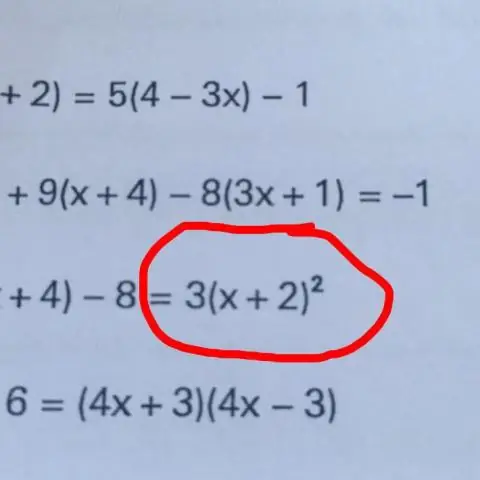
Айнымалыны оқшаулаудың негізгі әдісі теңдеудің екі жағын бірдей санға қосу, алу, көбейту немесе бөлу сияқты теңдеудің «екі жағына да бірдеңе жасау» болып табылады. Бұл процесті қайталау арқылы біз теңдеудің бір жағында оқшауланған айнымалыны аламыз
Теңдеуді немесе теңсіздікті қалай шешесіз?
Теңсіздікті шешу үшін келесі қадамдарды орындаңыз: 1-қадам Барлық мүшелерді барлық бөлшектердің ең кіші ортақ бөліміне көбейту арқылы бөлшектерді алып тастаңыз. 2-қадам Теңсіздіктің әр жағында ұқсас мүшелерді біріктіру арқылы жеңілдетіңіз. 3-қадам Бір жағында белгісізді, екінші жағында сандарды алу үшін шамаларды қосыңыз немесе азайтыңыз